ABC is an isosceles triangle AB=AC.Angle CAB =20 . D is a point on AB such that AD=BC . Find the angle ADC.

Let ABC is the given ISOSCELES triangle.  Where angle B=80, C=80,A=20 respectively. (in degrees)

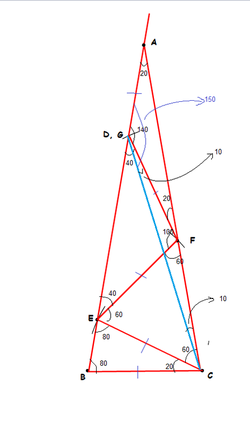
We need to find thae angle ADC where D is a point on AB such that AD = BC.
(Here after let us refer isosceles triangle is "iso")

SOLUTION:
 
Draw a line CE such that E is on AB and CE = BC. i,e, BCE is isosceles.
 
Observations: (all angles in degrees)
EBC= 80  , BEC = 80 (as triangle BCE is iso ) , BCE = 20 ( from triangle sum = 180)
ECF = BCF - BCE = 80 - 20 = 60

Draw a line EF such that F is on AC and EF = EC (which is = BC) . i,e, CEF is isosceles.
 
Observations: (all angles in degrees)
ECF= 60  , CFE = 60 (as triangle CEF is iso ) , CEF = 60 ( from triangle sum = 180)
From above all angles are 60. So CEF is equilateral.
So, FC = BC
GEF = 180 - ( BEC + CEF)  = 40

Draw a line FG such that G is on AB and FG = EF (which is = BC) . i,e, EFG is isosceles.
 
Observations: (all angles in degrees)
GEF= 40  , EGF = 40 (as triangle EFG is iso ) , EFG = 100 ( from triangle sum = 180)
AGF = 180 - EGF  = 180 - 40 = 140
AFG =  180 - ( CFE + EFG) = 20
We can see that GAF = AFG = 20 
                 so AGF is iso and AG = FG . But FG = BC 
So AG = BC. 
So G is our required point.

In triangle GFC, FG = FC =BC from above observations. hence GFE is iso. 
       so, angle FGE = FCE = 10 , (as GFE = 160 and sum of angles in triangle = 180)
Angle AGC = AGF + FGC 
   = 140 + 10 
=150 degrees.

P.S. : I observed it with different angles and found that there is unique answer for each angle of isosceles triangle. 
  Here angle A = 20, answer is ADC = 150
    A = 0   ->  ADC = 180 
    A = 20   ->  ADC = 150
    A = 40  ->  ADC = 100
    A = 60   ->  ADC = 60
    A = 80   ->  ADC = 40
         ........
If anyone can derive a generalised theorem to find it, please post it here or mail it.
..

---